問題文
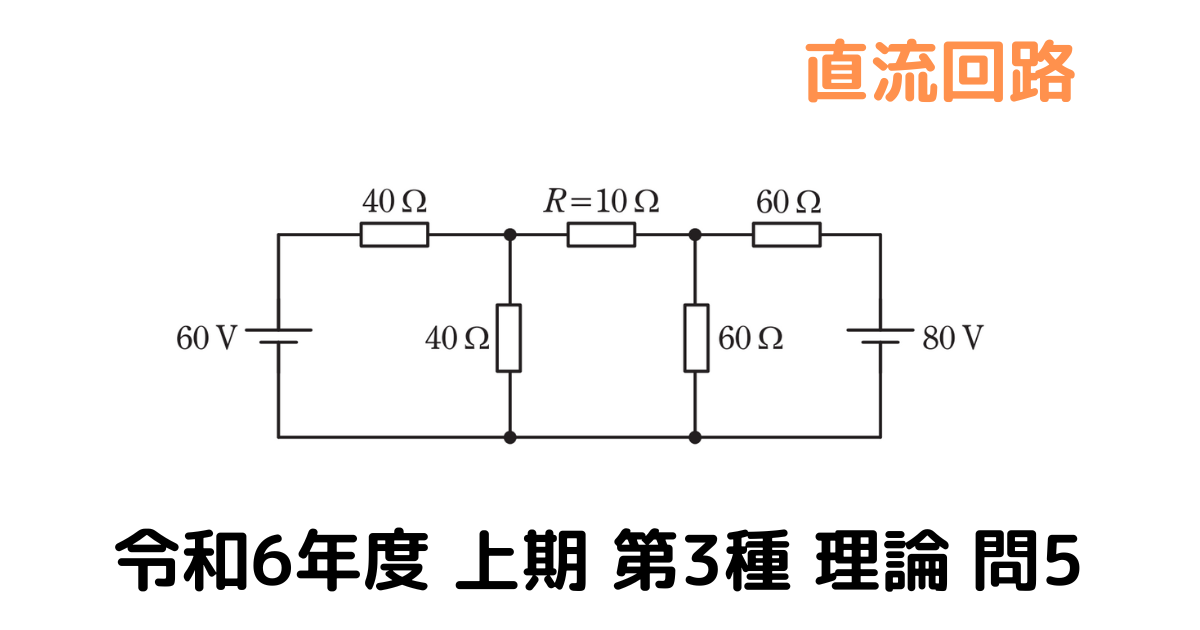
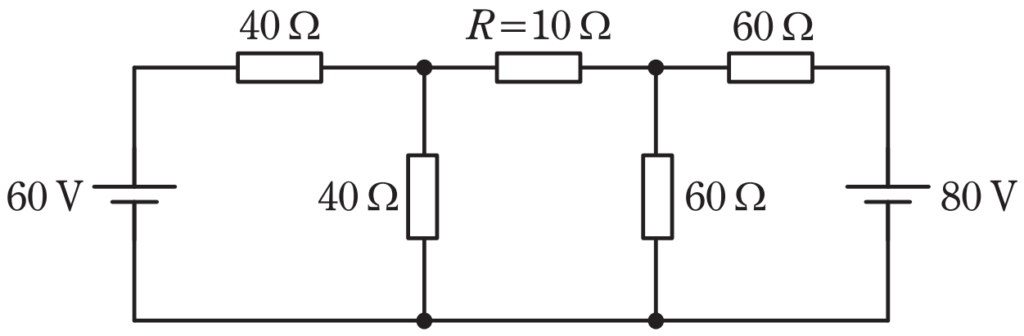
図の直流回路において,抵抗 \(\rm{R=10Ω}\)で消費される電力の値\(\rm{[W]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 0.28 (2) 1.89 (3) 3.79 (4) 5.36 (5) 7.62
プリントの配布
以下に、解説の内容を書き込めるプリントを配布しています。ノート代わりにダウンロードしてお使いください。
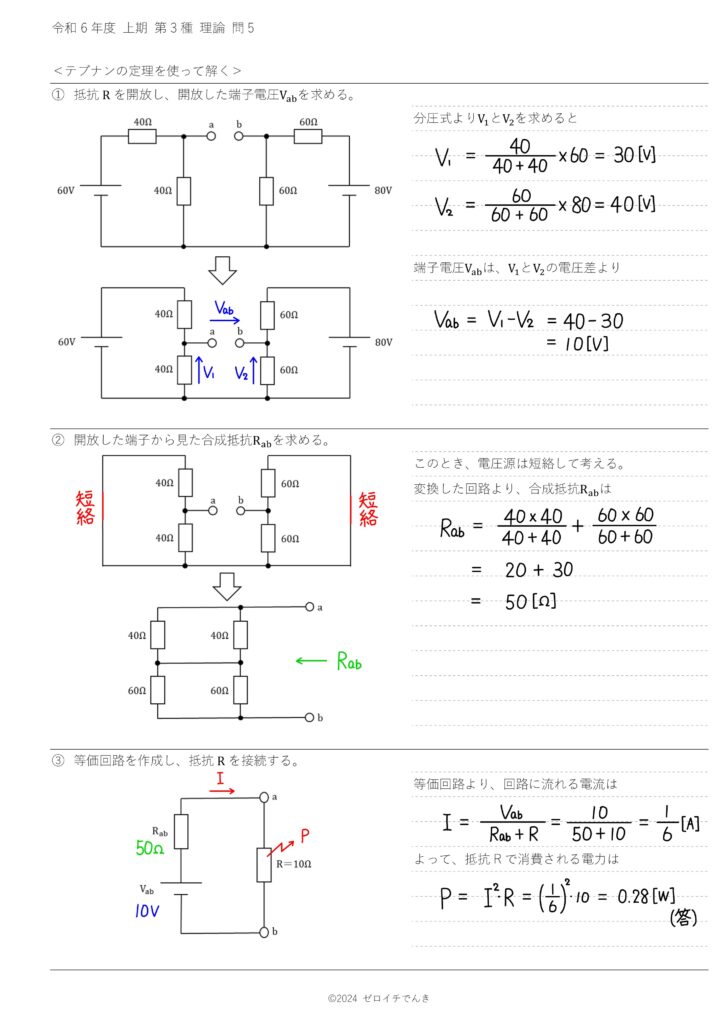
プリントの完成図はこちらです。ぜひ最後まで解説を読んでいってください。
解説
答え:(1)0.28
この問題は、テブナンの定理を使って解いていきます。
\(\rm{R=10Ω}\)に流れる電流を求めたいので、始めに\(\rm{R}\)を開放します(回路から取り外す)。
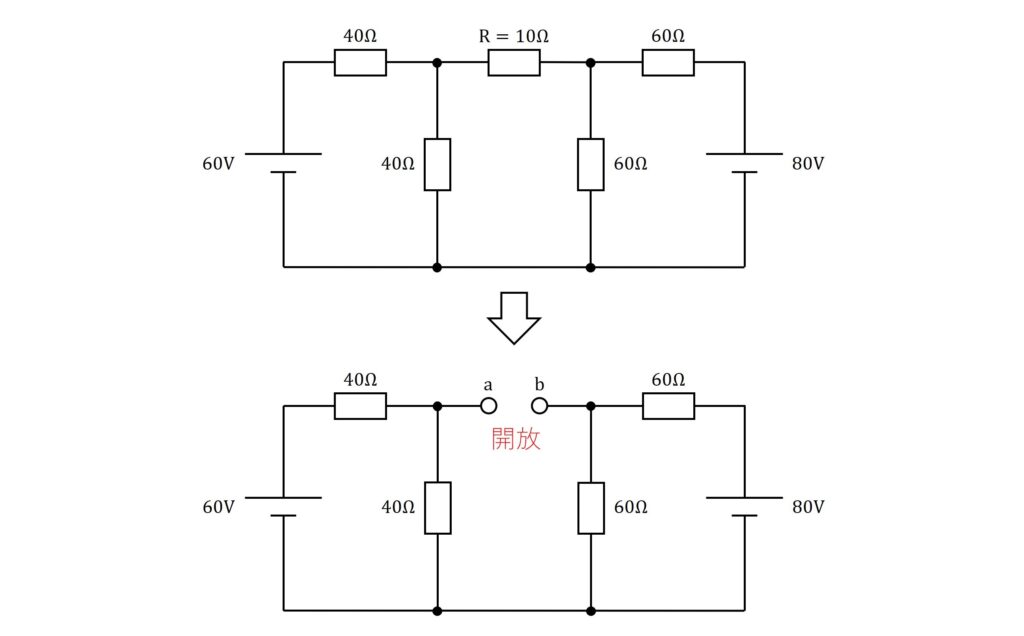
開放した端子にそれぞれ\(\rm{a,b}\)と名前を付けておきます。
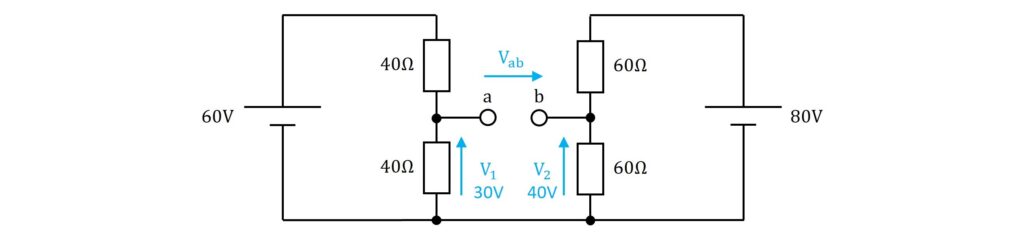
次に、回路を少し変形していきましょう。下図のように変形すると、回路の左側は\(\rm{60V}\)と\(\rm{40Ω}\)の抵抗2個の直列回路、回路の右側は\(\rm{80V}\)と\(\rm{60Ω}\)の抵抗2個の直列回路で構成されていることが分かります。
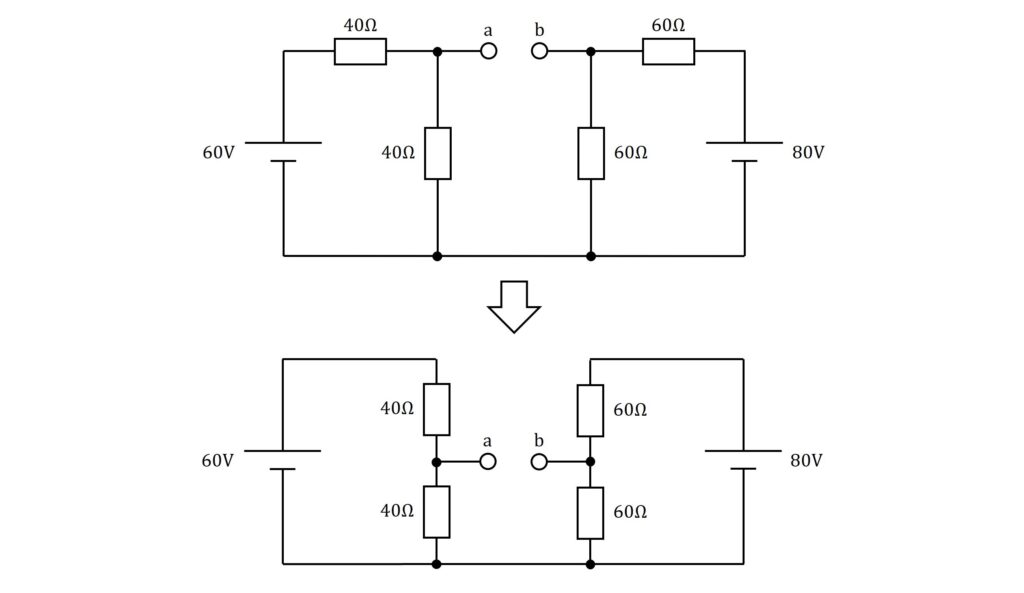
この回路をもとに、開放した端子間の電圧\(\rm{V_{ab}}\)を求めていきます。
\(\rm{V_{ab}}\)は、\(\rm{a}\)端子と\(\rm{b}\)端子の電位差(電圧差)であるから、\(\rm{40Ω}\)の抵抗に加わる電圧\(\rm{V_1}\)及び\(\rm{60Ω}\)の抵抗に加わる電圧\(\rm{V_2}\)を考えます。
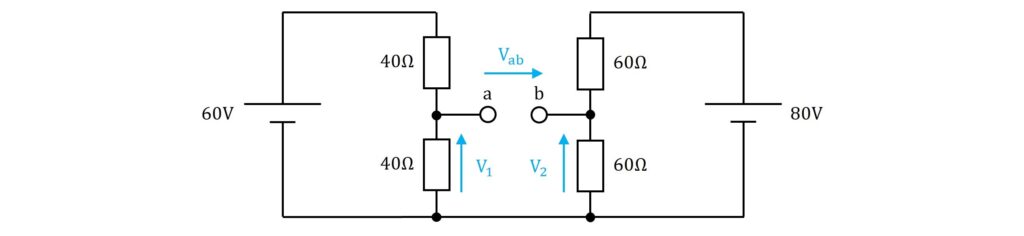
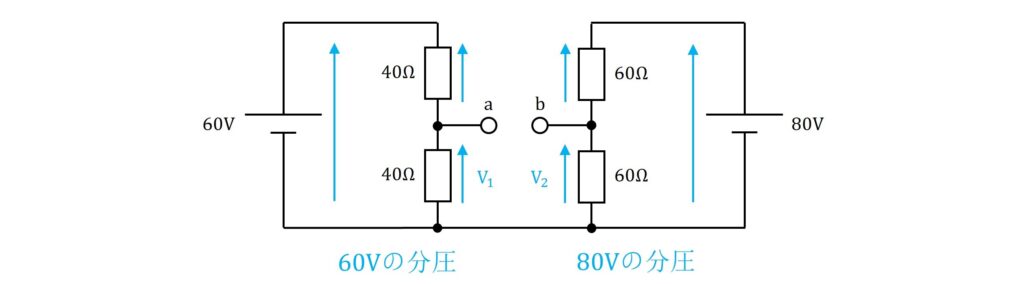
回路の左側は\(\rm{60V}\)の電圧を\(\rm{40Ω}\)の抵抗2個で分圧する形であり、回路の右側も\(\rm{80V}\)の電圧を\(\rm{60Ω}\)の抵抗2個で分圧する形になっています。
したがって、分圧式より\(\rm{V_1}\)、\(\rm{V_2}\)を求めると
\begin{eqnarray}
\rm{V_1}&=&\frac{40}{40+40}×60 \\[ 10pt ]
&=& \frac{40}{80}×60 \\[ 10pt ]
&=& \frac{1}{2}×60\\[ 10pt ]
&=& \rm{30[V]}
\end{eqnarray}
\begin{eqnarray}
\rm{V_2}&=&\frac{60}{60+60}×80 \\[ 10pt ]
&=& \frac{60}{120}×80 \\[ 10pt ]
&=& \frac{1}{2}×80\\[ 10pt ]
&=& \rm{40[V]}
\end{eqnarray}
端子間の電圧\(\rm{V_{ab}}\)は\(\rm{V_1}\)と\(\rm{V_2}\)の電位差であるから
\begin{eqnarray}
\rm{V_{ab}}&=& \rm{V_2}-\rm{V_1} \\[ 10pt ]
&=& 40-30 \\[ 10pt ]
&=& \rm{10[V]}
\end{eqnarray}
続いて、開放した端子\(\rm{a,b}\)から見た回路の抵抗について考えていきます。
回路には電圧源がありますが、電圧源を取り外した後、両端を短絡します。
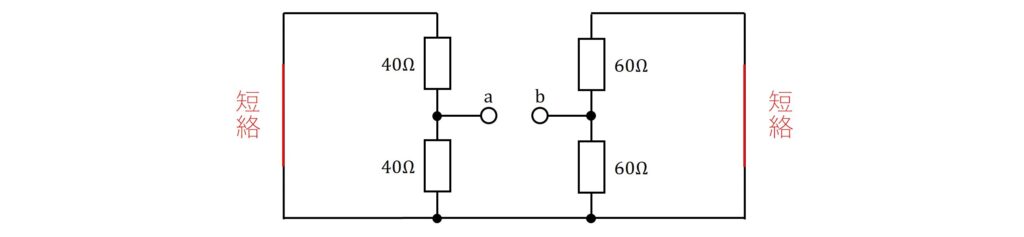
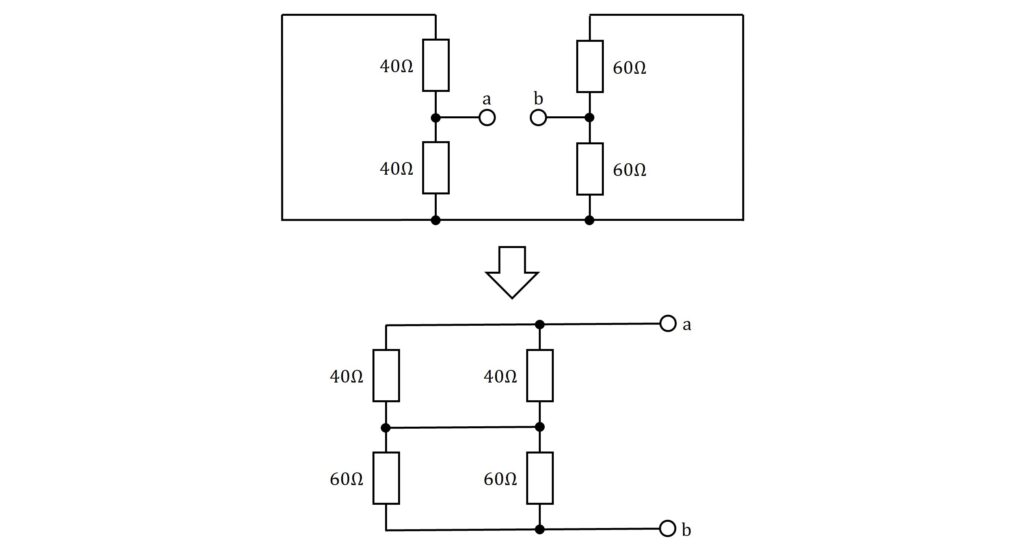
ここから回路を変形し、下図のように端子を右側へ引き出します。
すると、端子\(\rm{a,b}\)から見た回路は、\(\rm{40Ω}\)抵抗2個の並列接続と\(\rm{60Ω}\)抵抗2個の並列接続が直列に接続されていることが分かります。
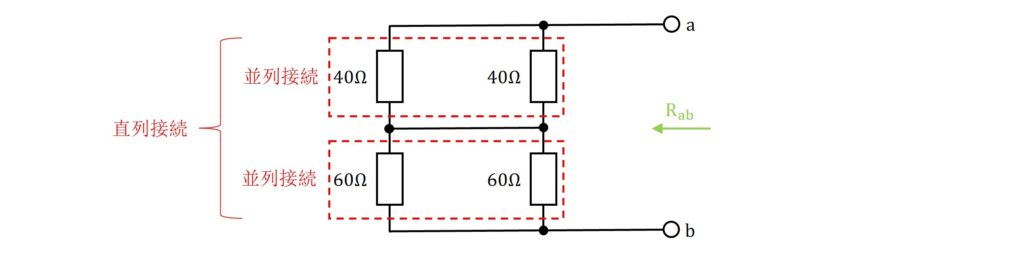
よって、端子\(\rm{a,b}\)から見た合成抵抗\(\rm{R_{ab}}\)は、
\begin{eqnarray}
\rm{R_{ab}}&=&\frac{40×40}{40+40}+\frac{60×60}{60+60} \\[ 10pt ]
&=&\frac{1600}{80}+\frac{3600}{120} \\[ 10pt ]
&=&20+30 \\[ 10pt ]
&=& \rm{50[Ω]}
\end{eqnarray}
最後に、テブナンの定理より等価回路を作成していきます。
上記で求めた電源電圧\(\rm{V_{ab}}\)および抵抗\(\rm{R_{ab}}\)と、始めに開放した抵抗\(\rm{R}\)を接続します。
作成した回路は、問題の回路を等価で表したものであり、抵抗\(\rm{R}\)に流れる電流も等しくなります。
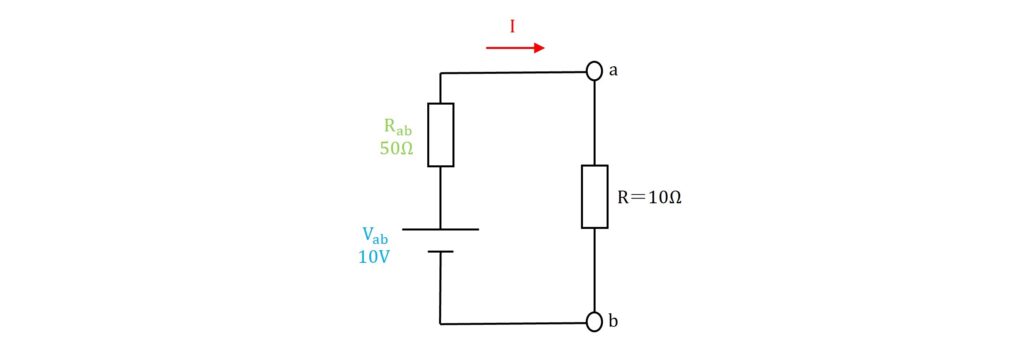
等価回路より、回路に流れる電流は
\begin{eqnarray}
\rm{I}&=&\frac{\rm{V_{ab}}}{\rm{R_{ab}}+\rm{R}} \\[ 10pt ]
&=& \frac{10}{50+10} \\[ 10pt ]
&=& \frac{1}{6}\rm{[A]}
\end{eqnarray}
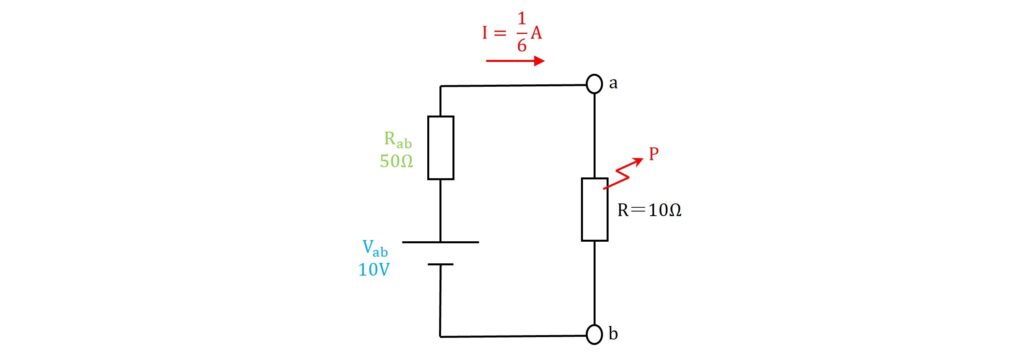
したがって、抵抗で発生する消費電力\(\rm{P}\)は、電力の公式を使って求めると
\begin{eqnarray}
\rm{P}&=&\rm{I^2・R}\\[ 10pt ]
&=&\left(\frac{1}{6}\right)^2×10\\[ 10pt ]
&=&\frac{10}{36}\\[ 10pt ]
&≒& 0.28\rm{[W](答)}
\end{eqnarray}