問題文
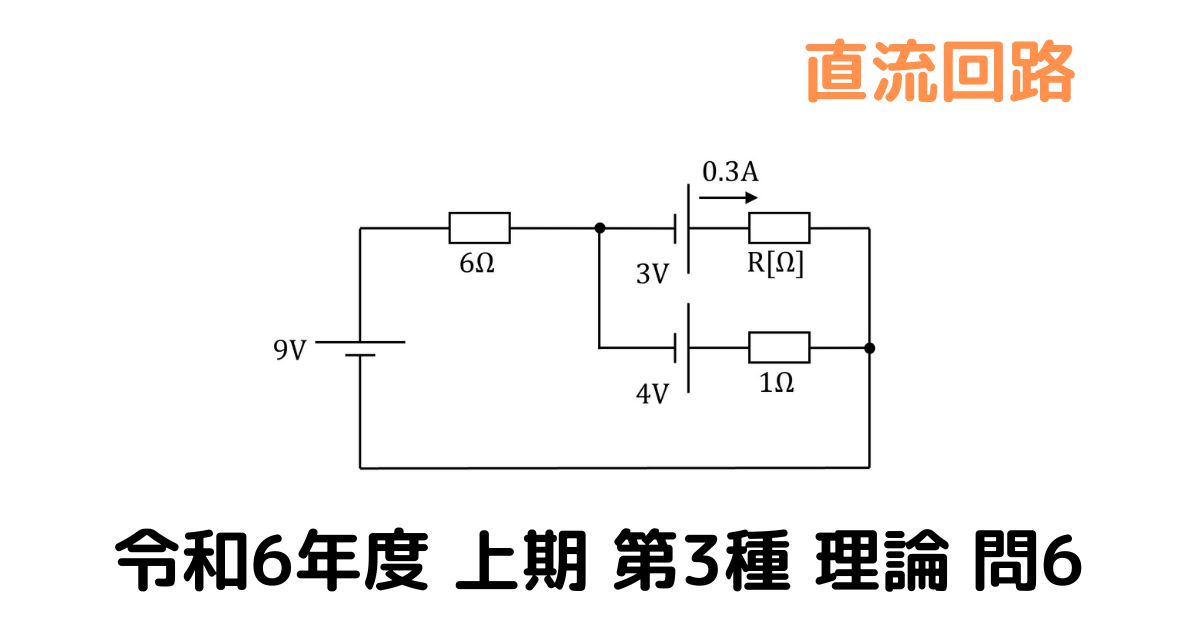
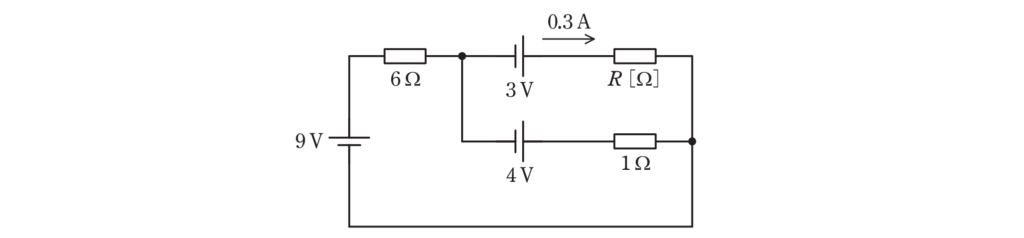
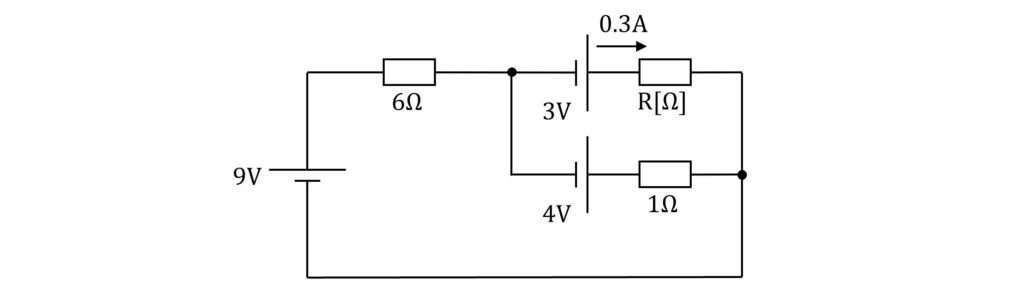
図の回路において,抵抗\(\rm{R[Ω]}\)には電流 \(\rm{0.3A}\)が流れている。抵抗 \(\rm{R}\)の値\(\rm{[Ω]}\)として,最も近いものを次の(1)~(5)のうちから一つ選べ。
(1) 2.0 (2) 2.8 (3) 3.7 (4) 4.9 (5) 25
プリントの配布
以下に、解説の内容を書き込めるプリントを配布しています。ノート代わりにダウンロードしてお使いください。
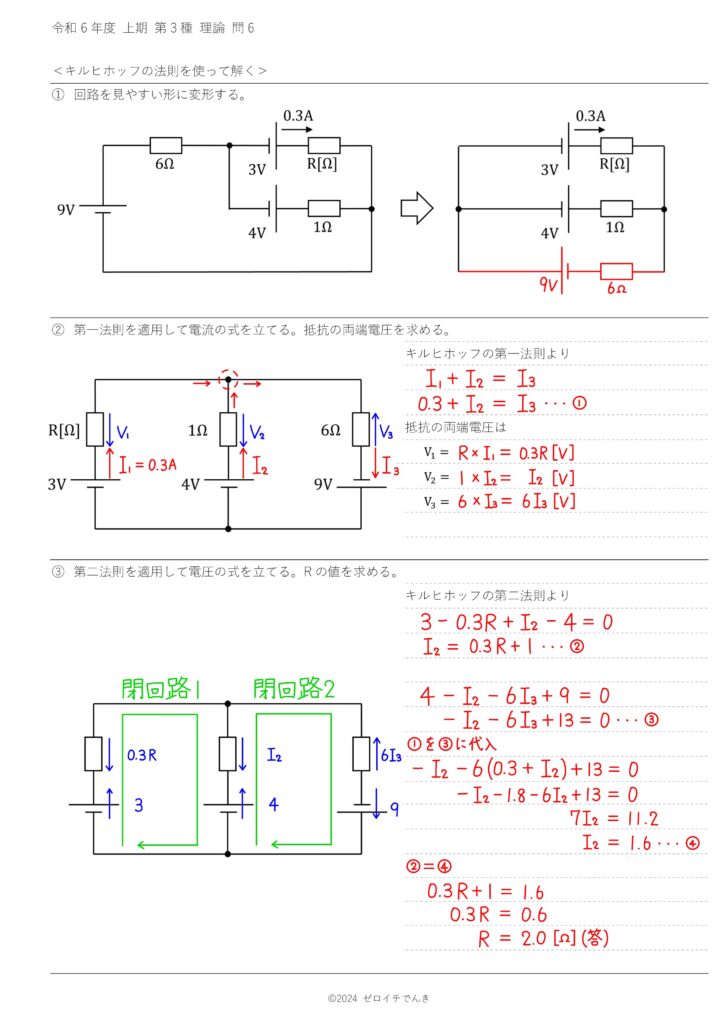
プリントの完成図はこちらです。ぜひ最後まで解説を読んでいってください。
解説
答え:(1)2.0
この問題では、キルヒホッフの法則を使って解いていきます。
まず、回路を見やすくするために\(\rm{6Ω}\)の抵抗と\(\rm{9V}\)の電源を移動させます。
移動する際、抵抗と電源の順番を入れ替えておりますが、直列では問題ありません。
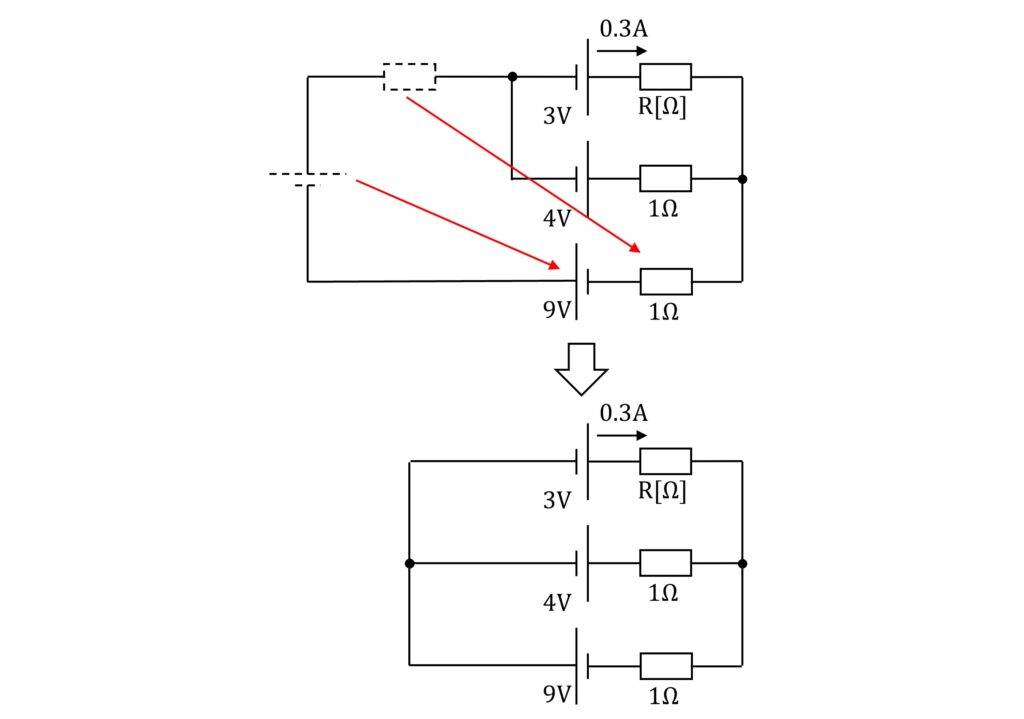
この回路をさらに横に傾けた状態で考えていきます。
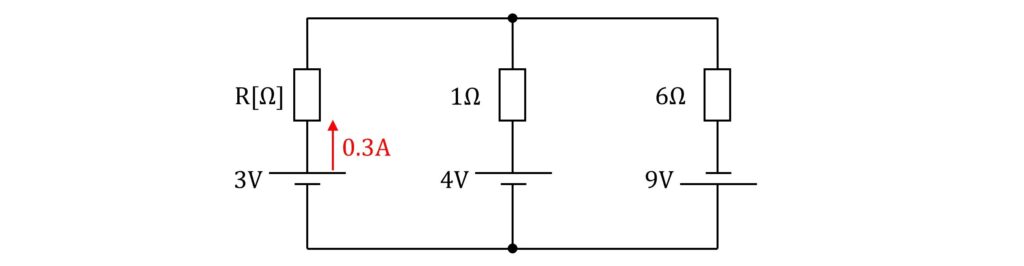
下準備として、この回路の各径路に流れる電流に名前を付けます。
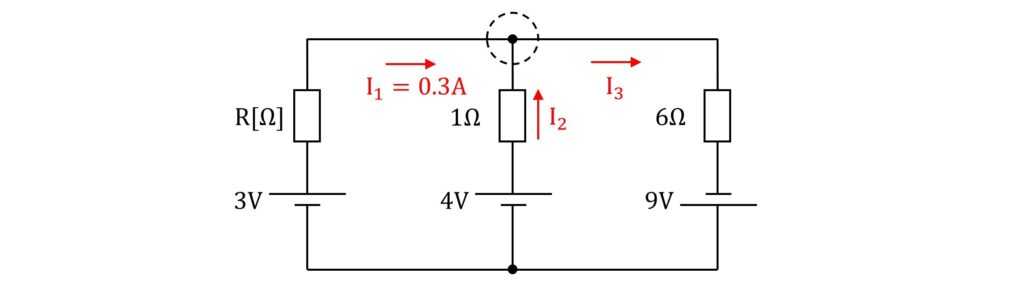
\(\rm{3V}\)に流れる電流を\(\rm{I_1}\)、\(\rm{4V}\)に流れる電流を\(\rm{I_2}\)、\(\rm{9V}\)に流れる電流を\(\rm{I_3}\)とします。
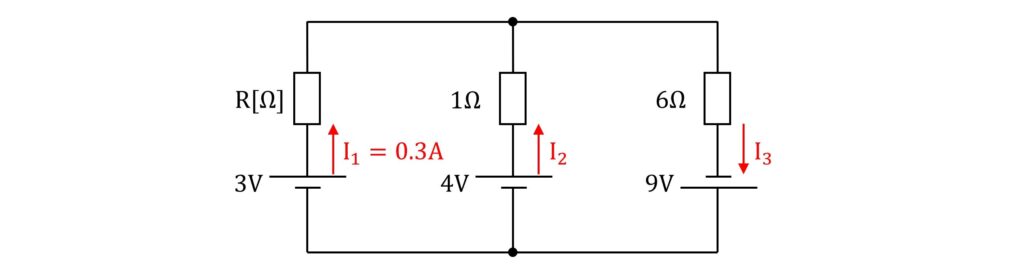
ここから、キルヒホッフの法則の第一法則と第二法則を適用していきます。
第一法則は、回路に流れる電流に関する法則です。
図のように、回路の接続点に着目して各径路に流れる電流の関係を表します。
第一法則より、接続点から見て流入する電流と流出する電流が等しくなります。よって、式で表すと
\begin{eqnarray}
\rm{I_1+I_2}&=&\rm{I_3}\\[ 10pt ]
\rm{0.3+I_2}&=&\rm{I_3・・・①}\\[ 10pt ]
\end{eqnarray}
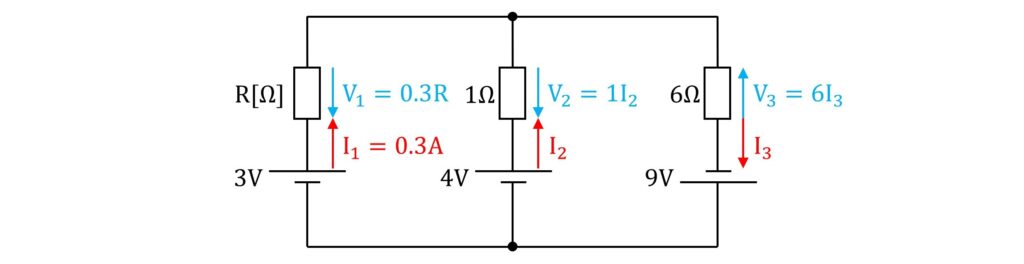
次に、抵抗の両端の電圧\(\rm{V_1}\)、\(\rm{V_2}\)、\(\rm{V_3}\)を求めていきます。
各径路にはそれぞれ\(\rm{I_1}\)、\(\rm{I_2}\)、\(\rm{I_3}\)が流れているので抵抗と掛け合わせると、
\begin{eqnarray}
\rm{V_1}&=&\rm{R×I_1=0.3R[V]}\\[ 10pt ]
\rm{V_2}&=&\rm{1×I_2=I_2[V]}\\[ 10pt ]
\rm{V_3}&=&\rm{6×I_3=6I_2[V]}\\[ 1pt ]
\end{eqnarray}
また、電圧方向の矢印は流れる電流とは反対方向に書きます。
さらに、電源電圧の電圧方向の矢印も書きます。電源電圧の場合は電源のプラス側に矢印を向けます。
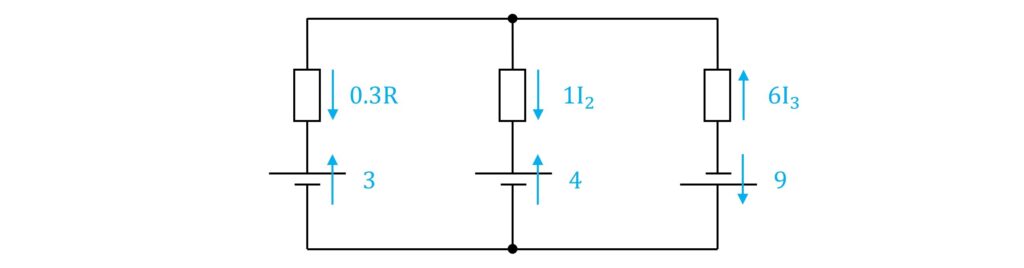
これをもとに、第二法則を適用していきます。第二法則は、回路の電圧に関する法則です。
回路を一巡する閉回路を書き、閉回路に沿って電圧の方向を確認していきます。
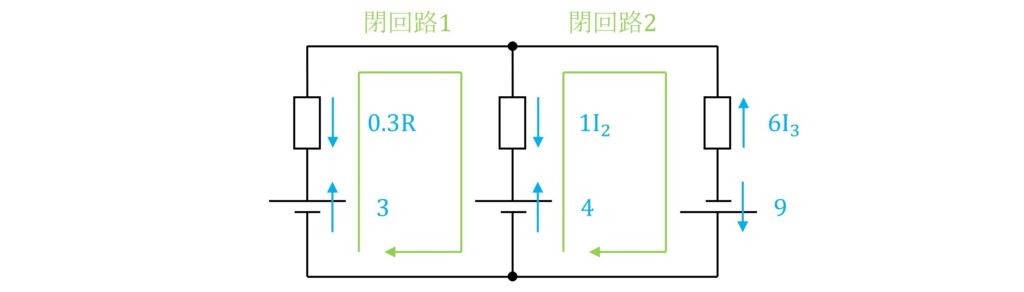
閉回路1を右回りで考えると、\(\rm{3[V]}\)と\(\rm{I_2[V]}\)は同方向、\(\rm{0.3R[V]}\)と\(\rm{4[V]}\)は逆方向です。
同方向の電圧をプラス、逆方向の電圧をマイナスとしたとき、第二法則より閉回路の電圧の合計=0という式を立てると、
\begin{eqnarray}
\rm{3-0.3R+I_2-4}&=&\rm{0}\\[ 10pt ]
\rm{I_2}&=&\rm{0.3R+1・・・②}\\[ 10pt ]
\end{eqnarray}
同じく、閉回路2より式を立てると、
\begin{eqnarray}
\rm{4-I_2-6I_3+9}&=&\rm{0}\\[ 10pt ]
\rm{-I_2-6I_3+13}&=&\rm{0・・・③}\\[ 10pt ]
\end{eqnarray}
また、①式は\(\rm{I_3}\)の式であるため、③の\(\rm{I_3}\)に代入すると、
\begin{eqnarray}
\rm{-I_2-6(0.3+I_2)+13}&=&\rm{0}\\[ 10pt ]
\rm{-I_2-1.8-6I_2+13}&=&\rm{0}\\[ 10pt ]
\rm{-7I_2+11.2}&=&\rm{0}\\[ 10pt ]
\rm{7I_2}&=&\rm{11.2}\\[ 10pt ]
\rm{I_2}&=&\rm{1.6・・・④}\\[ 10pt ]
\end{eqnarray}
よって、②式および④式は\(\rm{I_2}\)の式であるので、合わせると
\begin{eqnarray}
\rm{0.3R+1}&=&\rm{1.6}\\[ 10pt ]
\rm{0.3R}&=&\rm{1.6-1}\\[ 10pt ]
\rm{0.3R}&=&\rm{0.6}\\[ 10pt ]
\rm{R}&=&\rm{2.0[Ω](答)}\\[ 10pt ]
\end{eqnarray}