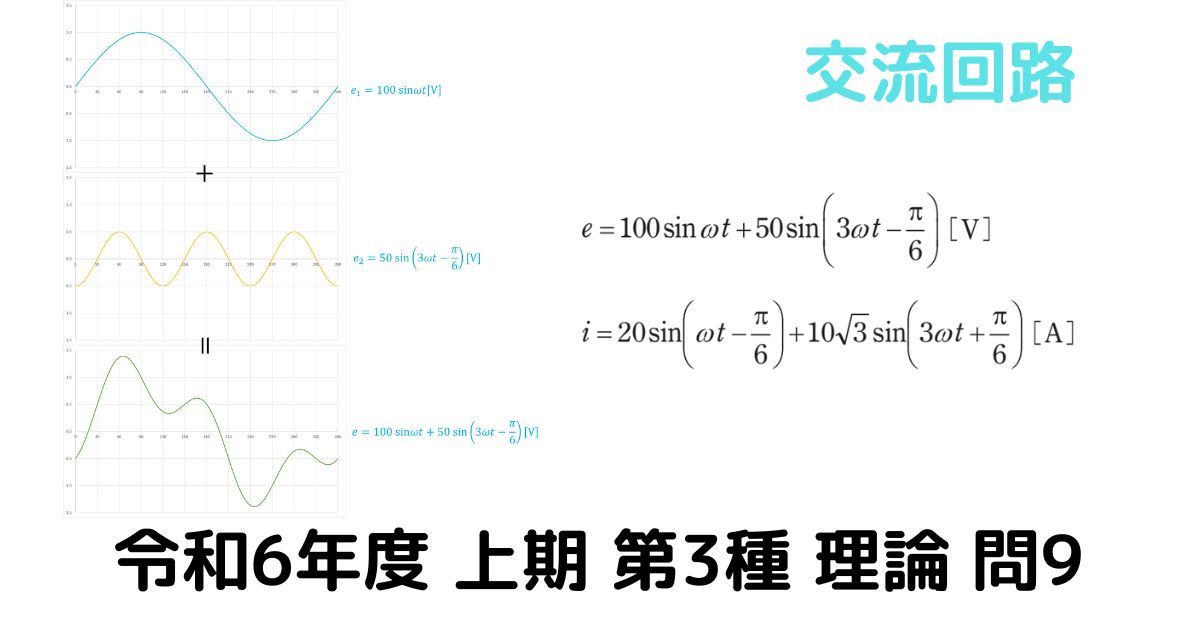
問題文
次式に示す電圧\(e\)\(\rm{[V]}\)及び電流\(i\)\(\rm{[A]}\)による電力の値\(\rm{[kW]}\)として、最も近いものを次の(1)~(5)のうちから一つ選べ。
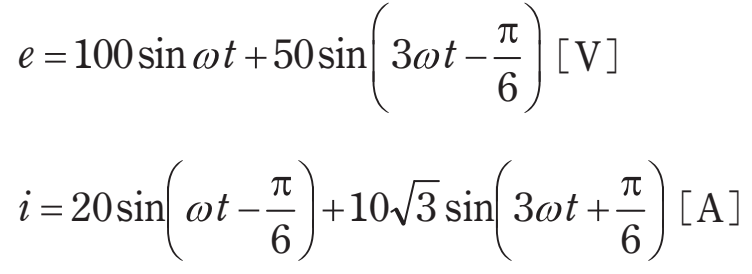
(1)0.95 (2)1.08 (3)1.16 (4)1.29 (5)1.34
プリントの配布
以下に、解説の内容を書き込めるプリントを配布しています。ノート代わりにダウンロードしてお使いください。
プリントの完成図はこちらです。ぜひ最後まで解説を読んでいってください。

解説
答え:(1)1.08
問題の電圧波形は、基本調波(\(\rm{sinωt}\))と第三調波(\(\rm{sin3ωt}\))の合成波形です。
第三調波とは、基本調波の3倍の周波数であり、基本調波との合成波形は下図のようになります。
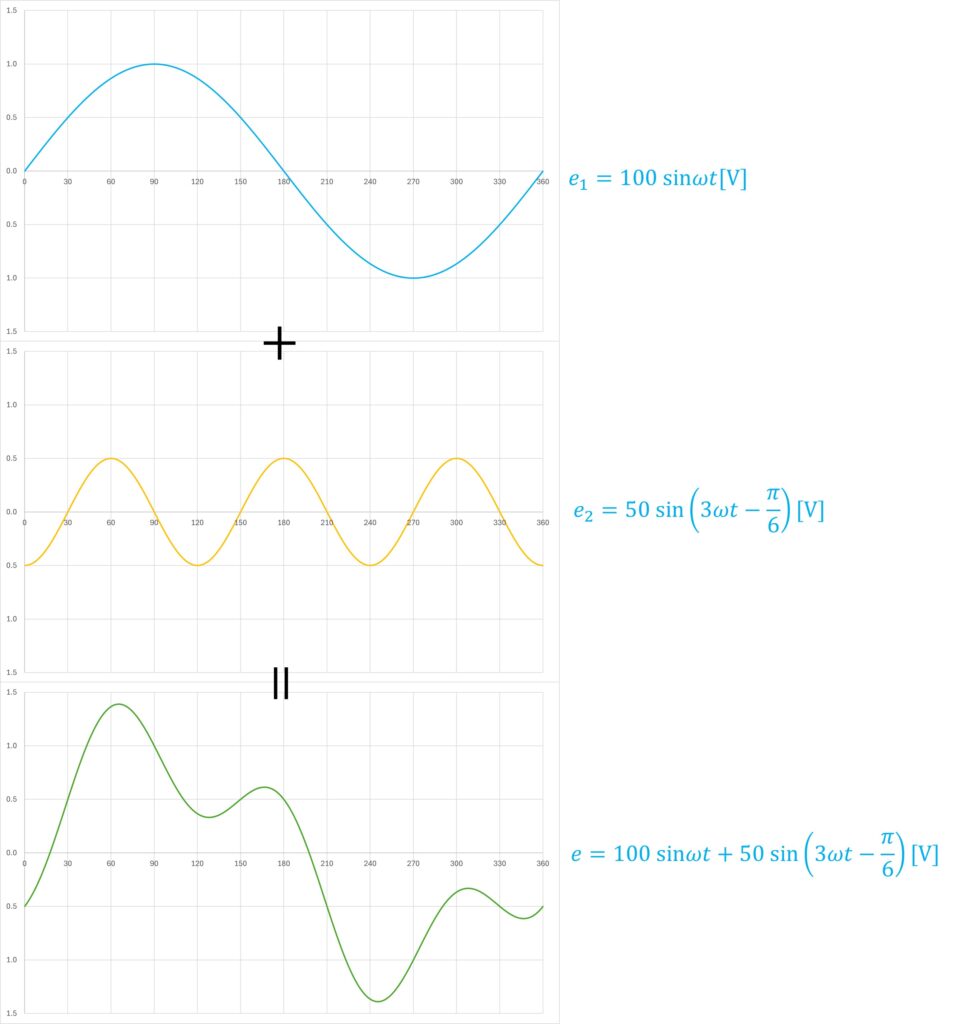
合成波形の状態では複雑であるため、基本調波回路と第三調波回路に分け、それぞれで考えていきます。
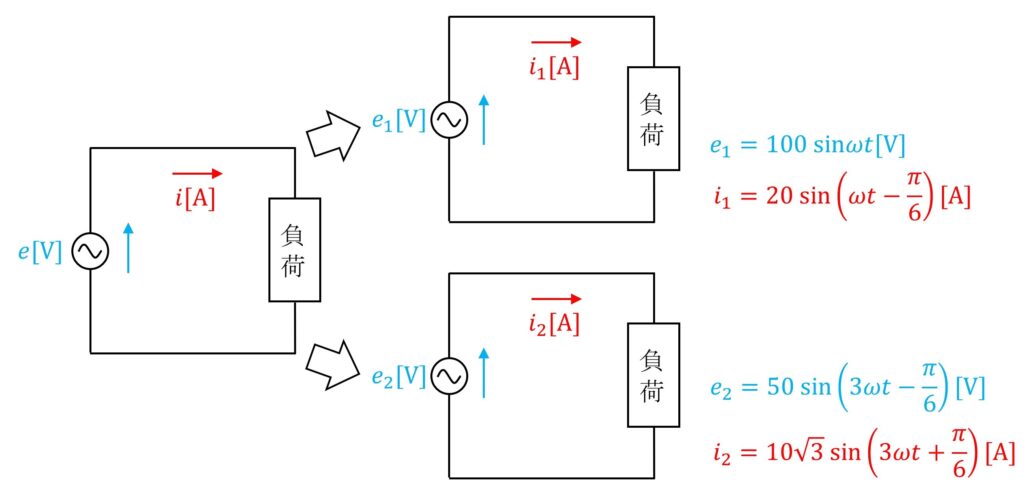
始めに、基本調波回路から求めていきます。
基本調波の瞬時値より、電圧・電流の実効値は最大値の\(\frac{1}{\sqrt{2}}\)倍であるため
\begin{eqnarray}
\rm{E_1}&=&\frac{100}{\sqrt{2}}\rm{[V]} \\[ 10pt ]
\rm{I_1}&=&\frac{20}{\sqrt{2}}\rm{[V]} \\[ 1pt ]
\end{eqnarray}
また、\(\rm{sinωt}\)を基準ベクトルとして電圧・電流のベクトルを描くと、下図となります。
電流は\(-\frac{π}{6}\)の位相差があり、遅れ(-)方向に30°回転した位置にあります。
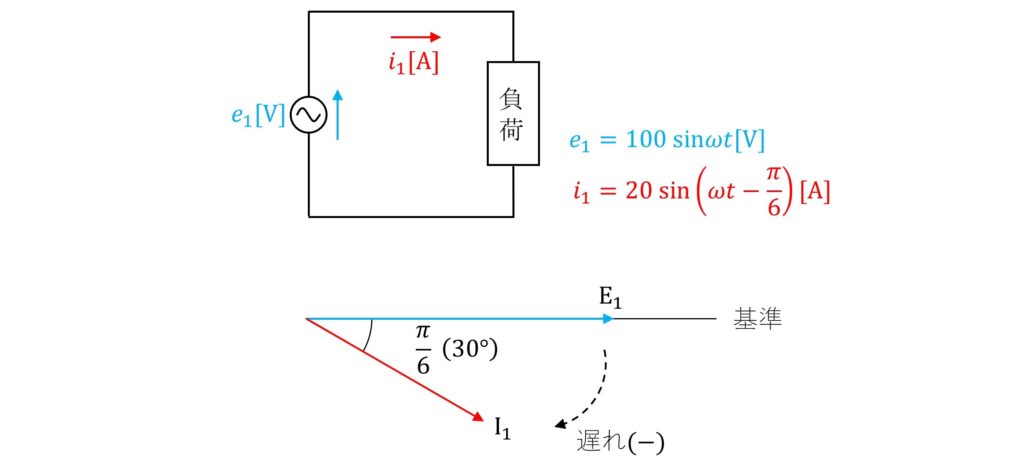
よって、基本調波回路で消費される電力\(\rm{P_1}\)は
\begin{eqnarray}
\rm{P_1}&=& \rm{E_1}×\rm{I_1}×\rm{cosθ_1} \\[ 10pt ]
&=& \frac{100}{\sqrt{2}}×\frac{20}{\sqrt{2}}×\frac{\sqrt{3}}{2} \\[ 10pt ]
&=& \frac{2000\sqrt{3}}{4} \\[ 10pt ]
&=& \rm{500\sqrt{3}[W]}\\[ 10pt ]
&=& \rm{0.5\sqrt{3}[kW]}
\end{eqnarray}
続いて、第三調波回路を求めていきます。
第三調波の瞬時値より、電圧・電流の実効値は
\begin{eqnarray}
\rm{E_2}&=&\frac{50}{\sqrt{2}}\rm{[V]} \\[ 10pt ]
\rm{I_2}&=&\frac{10\sqrt{3}}{\sqrt{2}}\rm{[V]} \\[ 1pt ]
\end{eqnarray}
また、\(\rm{sin3ωt}\)を基準ベクトルとして電圧・電流のベクトルを描くと、下図となります。
電圧は\(-\frac{π}{6}\)の位相差があり、遅れ(-)方向に30°回転した位置にあります。
電流は\(+\frac{π}{6}\)の位相差があり、進み(+)方向に30°回転した位置にあります。
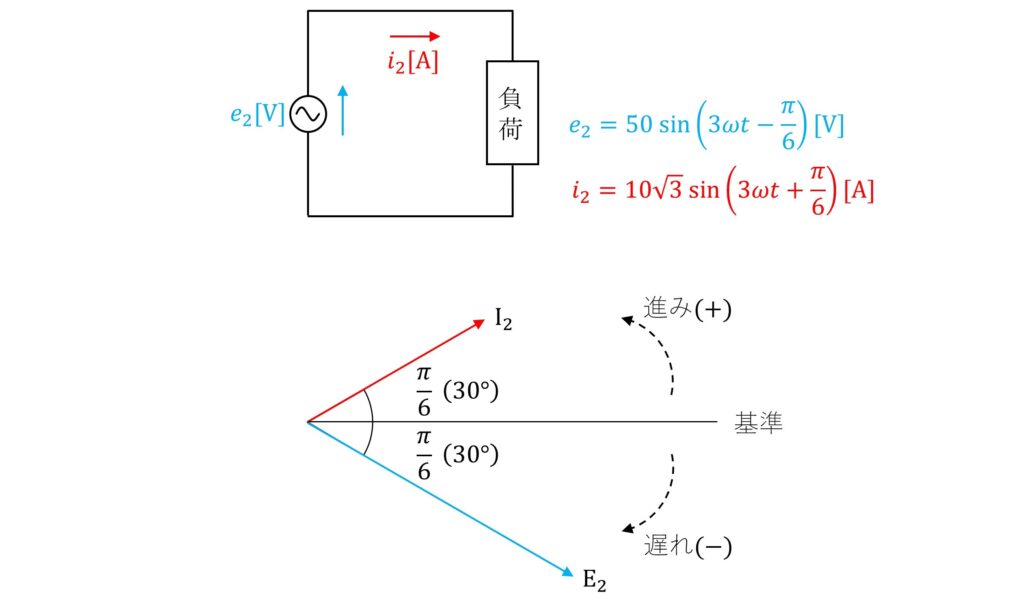
よって、電圧と電流の位相差は\(\rm{30°+30°=60°}\)であり、第三調波回路で消費される電力\(\rm{P_2}\)は
\begin{eqnarray}
\rm{P_2}&=& \rm{E_2}×\rm{I_2}×\rm{cosθ_2} \\[ 10pt ]
&=& \frac{50}{\sqrt{2}}×\frac{10\sqrt{3}}{\sqrt{2}}×\frac{1}{2} \\[ 10pt ]
&=& \frac{500\sqrt{3}}{4} \\[ 10pt ]
&=& \rm{125\sqrt{3}[W]}\\[ 10pt ]
&=& \rm{0.125\sqrt{3}[kW]}
\end{eqnarray}
よって、回路全体で消費される電力は
\begin{eqnarray}
\rm{P}&=& \rm{P_1}+\rm{P_2} \\[ 10pt ]
&=& \rm{0.5\sqrt{3}}+\rm{0.125\sqrt{3}} \\[ 10pt ]
&=& \rm{0.625\sqrt{3}} \\[ 10pt ]
&≒& \rm{1.08[kW](答)}
\end{eqnarray}